Задача №4 (Умение построить дерево игры по заданному алгоритму и обосновать выигрышную стратегию)

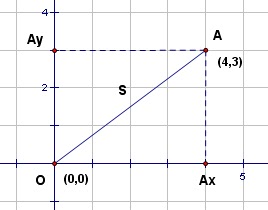
Два игрока играют в следующую игру. На координатной плоскости стоит фишка. Игроки ходят по очереди. В начале игры фишка находится в точке с координатами (4,3). Ход состоит в том, что игрок перемещает фишку из точки с координатами (x,y) в одну из трёх точек: или в точку с  (x+2, у), или в точку с координатами (x+3, у), или в точку с координатами (x, у+4). Выигрывает игрок, после хода которого расстояние от фишки до точки с координатами (0,0) не меньше 12 единиц. Кто выигрывает при безошибочной игре обоих партнёров — игрок, делающий первый ход, или игрок, делающий второй ход? Каким должен быть первый ход выигрывающего игрока? Ответ обоснуйте.

Решение: Для решения этого задания, необходимо знать как находится расстояние от фишки до точки с координатами (0,0).

Рис 1.

Рассмотрим нахождение расстояния от начальной позиции фишки (4,3) до точки с координатами (0,0). OAx = 4, OAy = 3. В силу теоремы Пифагора справедливо равенство
OAx² + OAy² = OA²
Соответственно,
То есть, расстояние от начальной позиции фишки (4,3) до точки с координатами (0,0) равно 
16 + 9 = 25. Извлекаем квадратный корень из 25, будет 5. Таким образом, проверяем расстояние на всех ходах.

Итак, давайте рассмотрим все потенциальные ходы обоих игроков.

1 ход - первый игрок

Начальная позиция	Ходы первого игрока
(4,3)	(6,3)
	(7,3)
	(4,7)

Таблица 1.

2 ход - второй игрок

Ходы первого игрока	Ходы второго игрока
(6,3)	(9,3)
	(8,3)
	(6,7)
(7,3)	(9,3)
	(10,3)
	(7,7)
(4,7)	(6,7)
	(7,7)
	(4,11)

Таблица 2.

3 ход - первый игрок

Повторяющиеся ходы второго игрока не рассматриваем.

Ходы второго игрока	Ходы первого игрока
(9,3)	(11,3)
	(12,3)
	(9,7)
(8,3)	(10,3)
	(11,3)
	(8,4)
(6,7)	(8,7)
	(9,7)
	(6,11)
(10,3)	(12,3)
	(13,3)
	(10,4)
(7,7)	(9,7)
	(10,7)
	(7,11)
(4,11)	(6,11)
	(7,11)
	(4,15)

Таблица 3.

Выделенные ходы являются выигрышными для первого игрока (так как расстояние от точки с координатами (0,0) больше или равно 12). Соответственно ходы: (9,3), (6,7), (10,3), (7,7) и (4,11) являются проигрышными для второго игрока. Он будет вынужден их совершить если первый игрок на первом ходу пойдёт: (7,3) или (4,7). Ответом на первый вопрос будет - при безошибочной игре выигрывает игрок, делающий первый ход. На третьем ходу первый игрок выигрывает. 

Ответом на второй вопрос будет - первый ход выигрывающего игрока (7,3) или (4,7), так как именно эти ходы приводит к проигрышным ходам для второго игрока на втором ходу.